맨위로가기

이진 힙

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

이진 힙은 이진 트리를 기반으로 하는 자료구조로, 힙 속성을 만족하며 삽입, 삭제, 최소/최대값 추출 등의 연산을 효율적으로 수행한다. 힙 연산에는 삽입, 추출, 삭제, 키 값 감소/증가 등이 있으며, 시간 복잡도는 O(log n)이다. 힙은 배열로 구현되며, 힙 구축에는 윌리엄스 방식과 플로이드 방식이 있다. 이진 힙은 d-ary 힙의 특수한 경우이며, 관련 자료 구조로는 d-항 힙, 최소-최대 힙, 이항 힙 등이 있다.

더 읽어볼만한 페이지

  • 힙 - 힙 (자료 구조)
    힙은 이진 트리 기반의 자료구조로, 부모 노드의 키 값이 자식 노드보다 크거나 작도록 구성되며, 최대 힙과 최소 힙이 존재하고, 배열로 구현되어 삽입, 삭제 연산의 시간 복잡도는 O(log n)이며, 다양한 분야에 활용된다.
  • 힙 - 이항 힙
    이항 힙은 이진 힙과 유사하며 이항 트리들의 집합으로 구현되어 최소 힙 속성을 만족하는 힙 자료 구조로, 특히 힙 병합 연산에서 효율적이며, 삽입, 삭제, 최소값 찾기 등의 연산을 지원하고 이산 사건 시뮬레이션 및 우선순위 큐 구현에 활용된다.
  • 이진 트리 - 스플레이 트리
    스플레이 트리는 스플레이 연산을 통해 자가 균형을 유지하며 최근 접근 노드의 빠른 접근을 가능하게 하는 이진 탐색 트리로, 분할 상환 분석 시 평균적으로 O(log n)의 시간 복잡도를 가진다.
  • 이진 트리 - 스레드 이진 트리
    스레드 이진 트리는 이진 트리의 NULL 포인터를 활용해 중위 순회 순서상 이전 또는 다음 노드를 가리키도록 하여 효율적인 순회를 가능하게 하고, 스레드 방식에 따라 단일 스레드와 이중 스레드로 나뉜다.
이진 힙
자료 구조
종류이진 트리/힙
고안자J. W. J. Williams
고안 연도1964년
성능
삽입 (최악)O(log n)
삽입 (평균)O(1)
최소값 삭제 (평균)O(log n)
최소값 삭제 (최악)O(log n)
키 감소 (평균)O(log n)
키 감소 (최악)O(log n)
최소값 찾기 (평균)O(1)
최소값 찾기 (최악)O(1)
병합 (평균)O(n)
병합 (최악)O(n)
참고 문헌
CLRS162–163쪽
Williams (1964)Algorithm 232 - Heapsort, Communications of the ACM, 7(6), 347–348
NarahariData Structures and Algorithms, Binary Heaps

2. 힙 연산

힙은 주로 삽입, 삭제, 검색, 키 값 변경 연산을 지원한다. 삽입과 제거 연산은 모두 힙의 모양 속성을 유지하기 위해 힙을 수정하고, 힙 속성은 힙을 위 또는 아래로 탐색하여 복원된다. 두 연산 모두 O(log n) 시간이 걸린다.

힙에서 루트를 삭제하는 과정은 다음과 같다.

1. 힙의 루트를 마지막 레벨의 마지막 요소로 바꾼다.

2. 새 루트를 자식과 비교한다. 순서가 맞으면 중지한다.

3. 그렇지 않으면 요소를 자식 중 하나와 바꾸고 이전 단계로 돌아간다. (최소 힙에서는 더 작은 자식과 바꾸고, 최대 힙에서는 더 큰 자식과 바꾼다.)

위의 2단계와 3단계를 '다운 힙(Down-heap)' 연산이라고도 부른다.

삽입 후 추출은 삽입 및 추출 함수를 단순히 호출하는 것보다 효율적으로 수행할 수 있다. 다운 힙 연산만 수행하는 방법은 다음과 같다.

1. 밀어넣는 항목과 힙의 맨 위를 비교한다.

2. 힙의 루트가 더 큰 경우:


  • 루트를 새 항목으로 바꾼다.
  • 루트부터 시작하여 다운 힙을 한다.

3. 그렇지 않으면 밀어넣는 항목을 반환한다.

파이썬은 삽입 후 추출을 위한 "heappushpop" 함수를 제공한다.[5][6]

2. 1. 삽입 (Insert)

새로운 요소를 힙의 마지막 레벨의 가장 왼쪽 빈 위치에 추가한다. 추가된 요소와 부모 노드를 비교하여 힙 속성을 만족할 때까지 위로 이동시킨다. 이 과정을 '상향 힙(Up-heap)' 또는 '버블 업(Bubble-up)'이라고 부른다.[3][4]

삽입 연산의 시간 복잡도는 O(log n)이다. (n은 힙의 요소 개수) 평균적인 경우, 삽입 연산은 O(1)의 상수 시간에 완료된다.[3][4]

최대 힙에 숫자 15를 삽입하는 예시는 다음과 같다.

15를 삽입하기 전


15와 8을 교환


15와 11을 교환 후


먼저 15를 X로 표시된 위치에 넣는다. 그러나 15 > 8 이므로 힙 속성이 위반되어 15와 8을 교환한다. 이후 15 > 11 이므로 다시 힙 속성이 위반되어 15와 11을 교환한다. 그러면 유효한 최대 힙이 된다.

2. 2. 추출 (Extract)

힙에서 루트 노드(최대 힙에서는 최댓값, 최소 힙에서는 최솟값)를 제거하는 과정은 다음과 같다.[1]

1. 힙의 루트 노드를 마지막 레벨의 마지막 요소와 바꾼다.

2. 새 루트 노드를 자식 노드들과 비교한다. 순서가 올바르면(최대 힙에서는 자식 노드보다 크거나 같고, 최소 힙에서는 작거나 같으면) 중지한다.

3. 그렇지 않으면, 새 루트 노드를 자식 노드 중 하나와 바꾼다. (최대 힙에서는 더 큰 자식과, 최소 힙에서는 더 작은 자식과 바꾼다.) 그리고 2단계로 돌아간다.

이러한 2, 3단계를 반복하여 힙 속성을 복원하는 과정을 '''다운 힙''' ('''버블 다운''', '''퍼컬레이트 다운''', '''시프트 다운''', '''싱크 다운''', '''트리클 다운''', '''힙화 다운''', '''캐스케이드 다운''' 등으로도 부른다) 연산이라고 한다.[1]

예를 들어, 다음과 같은 최대 힙이 있다고 가정하자.

최대 힙에서 11을 제거하기 전


여기서 11을 제거하고, 마지막 요소인 4를 루트 노드의 위치로 옮긴다.

최대 힙에서 11을 제거하고 4를 루트로 옮긴 후


이제 4는 자식 노드인 8보다 작으므로 힙 속성이 위반된다. 이 경우, 4와 8을 바꾸면 힙 속성이 복원된다.

4와 8을 교환하여 힙 속성을 복원한 후


최대 힙에서 아래로 이동하는 노드는 자식 노드 중 더 큰 자식과 교환되며, 최소 힙에서는 더 작은 자식과 교환된다. 이 과정은 새 루트 노드가 힙 속성을 만족할 때까지 반복된다.

이러한 다운 힙 연산은 배열로 구현된 힙에서 '''Max-Heapify''' (최대 힙의 경우) 또는 '''Min-Heapify''' (최소 힙의 경우) 함수로 수행할 수 있다. 이 함수의 의사코드는 다음과 같다 (배열 ''A''는 1부터 시작하는 인덱스를 사용).[1]

```

// 최대 힙에 대한 다운 힙 연산

// A: 힙을 나타내는 배열 (1부터 시작하는 인덱스)

// i: 힙화를 시작할 인덱스

Max-Heapify(A, i):

left ← 2 × i

right ← 2 × i + 1

largest ← i

if left ≤ length(A) and A[left] > A[largest] then:

largest ← left

if right ≤ length(A) and A[right] > A[largest] then:

largest ← right

if largest ≠ i then:

swap A[i] and A[largest]

Max-Heapify(A, largest)

```

위 알고리즘에서 인덱스 ''i''의 노드와 그 자식 노드들을 제외한 다른 노드들은 힙 속성을 만족해야 한다. 다운 힙 연산은 요소를 삭제하지 않고 루트 노드의 값을 수정하는 데에도 사용할 수 있다.[1]

새 루트 노드는 최악의 경우 힙의 가장 아래 레벨까지 이동해야 하므로, 추출 연산의 시간 복잡도는 힙의 높이에 비례하는 O(log ''n'')이다.[1]

2. 3. 삽입 후 추출 (Insert then extract)

파이썬은 삽입 후 추출을 위한 "heappushpop" 함수를 제공한다. 힙 배열은 첫 번째 요소의 인덱스가 1이라고 가정한다.[5][6]

```python

# 새 항목을 (최대) 힙에 푸시한 다음 결과 힙의 루트를 추출한다.

# 'heap': 힙을 나타내는 배열, 인덱스 1에서 시작

# 'item': 삽입할 요소

# 'item'과 'heap'의 루트 중 더 큰 값을 반환한다.

def push_pop(heap, item):

if heap and heap[0] > item: # 최소 힙인 경우 <

heap[0], item = item, heap[0]

_downheap(heap, 0)

return item

```

파이썬에서 "heapreplace"라고 하는, 추출한 다음 삽입을 하는 유사한 함수도 정의할 수 있다.

```python

# 힙의 루트를 추출하고 새 항목을 푸시한다.

# 'heap': 힙을 나타내는 배열, 인덱스 1에서 시작

# 'item': 삽입할 요소

# 'heap'의 현재 루트를 반환한다.

def replace(heap, item):

heap[0], item = item, heap[0]

_downheap(heap, 0)

return item

2. 4. 검색 (Search)

임의의 요소를 찾는 데는 O(n) 시간이 걸린다.

2. 5. 삭제 (Delete)

임의의 요소를 삭제하는 과정은 다음과 같다.

1. 삭제할 요소의 인덱스 i를 찾는다.

2. 해당 요소를 힙의 마지막 요소와 교환하고, 마지막 요소는 제거한다.

3. 힙 속성을 복원하기 위해 다운 힙(down-heap) 또는 업 힙(up-heap) 연산을 수행한다. 최대 힙에서는 요소 i의 새 키 값이 이전 키 값보다 클 때만 업 힙을 수행하면 된다. 이는 부모 노드의 힙 속성만 위반될 수 있기 때문이다. 반대로 최소 힙에서는 새 키 값이 이전 키 값보다 작을 때만 업 힙을 수행하면 된다. 요소 교환 전, 요소 i와 그 자식 요소들 사이에 힙 속성이 이미 만족되었다고 가정하면, 키 값이 더 커지거나(최대 힙) 작아져도(최소 힙) 힙 속성은 여전히 유지되기 때문이다. 새 키 값이 이전 키 값보다 작을(최대 힙) 때는 다운 힙만, 클 때는(최소 힙) 업 힙만 필요하다. 그 이유는 힙 속성이 자식 노드에서만 위반될 수 있기 때문이다.

나무 구조를 배열로 관리할 때는, 노드와 배열 번호 간의 대응 관계를 별도로 관리해야 한다. 연관 배열을 사용하거나, 각 노드에 배열 번호를 포함하거나, 나타나는 노드가 한정되어 있다면 일반 배열을 사용할 수도 있다.

삭제 절차는 다음과 같다.

1. 삭제된 노드가 이미 힙의 말단 노드(배열의 마지막 요소)라면, 추가 작업 없이 바로 종료한다.

2. 힙의 말단 노드를 빈 자리로 옮기고, 다운 힙을 수행한다.

3. 위 과정에서 힙 구조가 변하지 않았다면, 업 힙을 수행한다.

2. 6. 키 값 감소/증가 (Decrease/Increase Key)

키 값 감소/증가 연산은 주어진 요소의 키 값을 변경하는 연산이다. 감소 키 연산은 주어진 노드의 값을 더 작은 값으로, 증가 키 연산은 더 큰 값으로 대체한다. 이 연산에는 주어진 값을 가진 노드를 찾고, 값을 변경한 다음, 힙 속성을 복원하기 위해 아래로 힙 정렬(Down-heap) 또는 위로 힙 정렬(Up-heap)을 수행하는 과정이 포함된다.[1]

최대 힙을 기준으로, 감소 키 연산 및 증가 키 연산은 다음과 같이 수행할 수 있다.[1]

연산 종류수행 과정
감소 키 연산
증가 키 연산



값의 갱신은 다익스트라 알고리즘이나 A* 알고리즘 등에서 사용된다. 최대 힙의 경우, 노드의 값을 갱신한 후, 값이 증가하면 Up-heap을 하고, 값이 감소하면 Down-heap을 수행하여 힙 속성을 복원할 수 있다. 계산량은 늘어나지만, 삭제 후 추가로 구현하는 것도 가능하다.[1]

3. 힙 구축 (Building a Heap)

n개의 입력 요소를 가진 배열에서 힙을 구축하는 방법에는 윌리엄스(Williams) 방식과 플로이드(Floyd) 방식이 있다.


  • 윌리엄스(Williams) 방식: 빈 힙에서 시작하여 각 요소를 차례대로 삽입한다. 이 방식은 이진 힙을 발명한 윌리엄스의 이름을 딴 것이다. 각 삽입에 $O(\log n)$ 비용이 들기 때문에, $n$번의 삽입을 통해 $O(n \log n)$ 시간에 힙이 구축된다.[7] 평균적인 경우에는 선형 시간이 걸린다.[8]

  • 플로이드(Floyd) 방식: 윌리엄스 방식보다 더 빠른 방법이다. 임의의 이진 트리에 요소를 배치하여 모양 속성을 존중하는 것으로 시작한다. (트리는 배열로 나타낼 수 있다.) 그런 다음 가장 낮은 레벨부터 시작하여 위로 이동하면서 각 서브트리의 루트를 아래로 이동시켜 힙 속성을 복원한다. 높이 $h$에서 시작하는 모든 서브트리가 이미 "힙화"된 경우, 높이 $h+1$의 트리는 최대 힙을 구성할 때는 가장 큰 값을 가진 자식 경로를 따라, 최소 힙을 구성할 때는 가장 작은 값을 가진 자식 경로를 따라 루트를 보내 힙화할 수 있다. 이 과정은 노드당 $O(h)$ 연산(스왑)이 필요하다. 이 방법에서는 힙화의 대부분이 하위 레벨에서 수행된다. 높이 $h$의 노드 수는 $\le \frac{n}{2^h}$이므로, 모든 서브트리를 힙화하는 데 드는 비용은 $O(n)$이다.


:

\begin{align}

\sum_{h=0}^{\lfloor \log n \rfloor} \frac{n}{2^h} O(h)

& = O\left(n\sum_{h=0}^{\lfloor \log n \rfloor} \frac{h}{2^h}\right) \\

& = O\left(n\sum_{h=0}^{\infty} \frac{h}{2^h}\right) \\

& = O(n)

\end{align}



힙 구성 중 최악의 경우 비교 횟수는 $2n - 2s_2(n) - e_2(n)$이다.[9] 여기서 $s_2(n)$은 $n$의 이진 표현의 모든 자릿수의 합이고, $e_2(n)$은 $n$의 소인수 분해에서 2의 지수이다. 평균적인 경우에는 점근적으로 $1.8814n - 2 \log_2 n + O(1)$ 비교에 접근한다.[10][11]

'''Build-Max-Heap''' 함수는 ''n''개의 노드를 가진 완전 이진 트리를 저장하는 배열 ''A''를 최대 힙으로 변환한다. '''Build-Max-Heap'''는 나머지 트리의 각 노드에서 '''Max-Heapify'''를 실행한다.

'''Build-Max-Heap''' (''A''):

'''for each''' index ''i'' '''from''' ''floor''(''length''(''A'')/2) '''downto''' 1 '''do:'''

'''Max-Heapify'''(''A'', ''i'')

4. 힙 구현 (Heap Implementation)

힙은 주로 배열을 사용하여 구현한다. 이진 힙은 항상 완전 이진 트리이므로, 포인터를 위한 공간이 필요 없이 콤팩트하게 저장할 수 있다. 각 노드의 부모와 자식은 배열 인덱스에 대한 산술 연산을 통해 찾을 수 있다. 이러한 속성 덕분에 힙 구현은 암시적 자료 구조의 한 예시가 된다.

''n''을 힙의 요소 수, ''i''를 배열의 유효한 인덱스라고 할 때, 루트 노드의 인덱스 위치에 따라 다음과 같이 부모/자식 노드를 찾을 수 있다.


  • 루트 노드가 인덱스 0에 있는 경우 (유효 인덱스: 0 ~ ''n''-1):
  • 인덱스 ''i''인 요소의 자식 노드: 인덱스 2''i'' + 1, 2''i'' + 2
  • 인덱스 ''i''인 요소의 부모 노드: 인덱스 ''floor''((''i'' - 1) / 2)
  • 루트 노드가 인덱스 1에 있는 경우 (유효 인덱스: 1 ~ ''n''):
  • 인덱스 ''i''인 요소의 자식 노드: 인덱스 2''i'', 2''i'' + 1
  • 인덱스 ''i''인 요소의 부모 노드: 인덱스 ''floor''(''i'' / 2)


이진 힙과 배열 구현의 비교


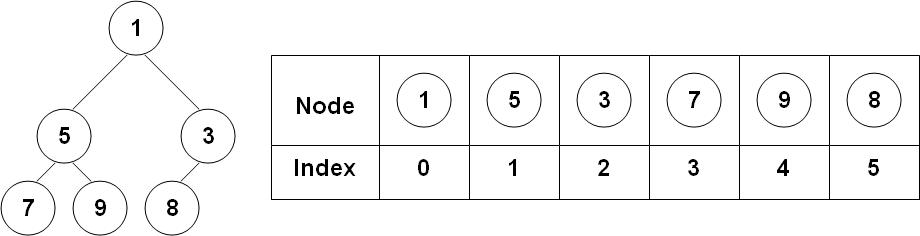
이러한 구현 방식은 힙을 저장하기 위해 입력 배열의 공간을 재사용하는 힙 정렬 알고리즘에 사용된다. 또한, 동적 배열을 사용하면 무제한으로 항목을 삽입할 수 있어 우선순위 큐로도 유용하다.

두 개의 이진 힙을 병합하는 연산은 크기가 같은 힙의 경우 Θ(''n'')이 걸린다. 따라서 단순히 두 힙 배열을 연결하고, 그 결과에 대해 힙을 만드는 것이 최선이다.[13] 만약 병합이 빈번하게 일어나는 연산이라면, O(log ''n'') 시간에 병합할 수 있는 이항 힙과 같은 다른 힙 구현을 사용하는 것이 좋다.

5. 관련 자료 구조

이진 힙은 d-ary 힙의 특수한 경우로, d = 2인 경우이다. 즉, 각 노드는 최대 두 개의 자식을 가질 수 있다. 일반적인 배열 기반 힙에서 한 노드의 두 자식은 힙 속성을 위반하지 않는 한 자유롭게 교환될 수 있지만, 힙 속성을 유지하기 위해 자식의 하위 트리 노드를 이동해야 할 수도 있다.

6. 실행 시간 요약

계산량 (최대 힙)
연산최악의 경우평균
최댓값 얻기O(1)O(1)
요소 수 얻기O(1)O(1)
추가O(log n)O(1)
삭제O(log n)O(log n)
값 갱신O(log n)O(1)



평균 계산량뿐만 아니라 최악의 경우에도 O(1)으로 만들고 싶다면, 다른 힙 구조를 고려해야 하지만, 이진 힙을 배열로 구현했을 경우, 계산량의 상수항이 일반적으로 다른 알고리즘보다 작고, 현실적으로는 이진 힙이 가장 빠른 경우도 많으며, libstdc++ (gcc)의 priority_queue 구현에서는 기본형의 경우 이진 힙 사용을 권장하고 있다[17]. 피보나치 힙을 사용하면, 평균 계산량이 아닌 상환 계산량으로, 추가 및 갱신은 O(1), 삭제는 O(log n)이 된다.

참조

[1] 간행물 Algorithm 232 - Heapsort
[2] citation Data Structures and Algorithms https://gtl.csa.iisc[...]
[3] 간행물 Random insertion into a priority queue structure 1975-09
[4] 간행물 Data structures https://publikatione[...] 1989-02
[5] 웹사이트 python/cpython/heapq.py https://github.com/p[...] 2020-08-07
[6] 웹사이트 heapq — Heap queue algorithm — Python 3.8.5 documentation https://docs.python.[...] 2020-08-07
[7] 서적 Introduction to Algorithms
[8] 간행물 Average Case Analysis of Heap Building by Repeated Insertion http://www.stats.ox.[...] 2016-01-28
[9] citation Elementary Yet Precise Worst-Case Analysis of Floyd's Heap-Construction Program http://www.deepdyve.[...]
[10] 간행물 An Average Case Analysis of Floyd's Algorithm to Construct Heaps https://core.ac.uk/d[...] 1984-05
[11] 간행물 Elementary Average Case Analysis of Floyd's Algorithm to Construct Heaps Turku Centre for Computer Science 1996-11
[12] 간행물 You're Doing It Wrong http://queue.acm.org[...] 2010-06-11
[13] 웹사이트 binary heap http://nist.gov/dads[...] 2008-08-08
[14] 간행물 An Algorithm for Merging Heaps https://doi.org/10.1[...]
[15] 간행물 A characterization of heaps and its applications
[16] 웹사이트 Min-max heaps and generalized priority queues. http://cg.scs.carlet[...] Programming techniques and Data structures. Comm. ACM, 29(10): 996–1000 1986-10-01
[17] 웹사이트 Priority-Queue Design https://gcc.gnu.org/[...]
[18] 웹사이트 ヒープの正体」（たなかともひさ） http://www.maroontre[...]


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com